Когнитивное моделирование в задачах анализа и управления
слабоструктурированными системами – это исследование функционирования
и развития слабоструктурированных систем
и ситуаций посредством построения модели на
основе когнитивной карты. В этой модели когнитивная карта отражает
субъективные представления (индивидуальные
или коллективные) исследуемой проблемы,
ситуации, связанной с функционированием и развитием
слабоструктурированной системы. Основными элементами когнитивной карты являются базисные факторы (или просто факторы)
и причинно-следственные связи между ними. Когнитивная карта строится на
основании субъективных представлений экспертов о ситуации.
Формальное определение нечеткой когнитивной карты
Нечеткая
когнитивная модель основана на формализации причинно-следственных связей,
которые имеют место между факторами (переменными, параметрами),
характеризующими исследуемую систему. Результатом формализации является
представление системы в виде причинно-следственной сети, называемой нечеткой
когнитивной картой и имеющей вид:
G=< E, W >,
где E = {e1, e2, …, en
} – множество факторов (также называемых концептами), W – нечеткое причинно-следственное отношение на множестве E.
Элементы wij ∈ W(i
,j = 1, …, n) характеризуют направление и степень интенсивности (вес) влияния между концептами
ei и ej:
wij = w(ei, ej),
где w
– показатель интенсивности влияния (характеристическая функция отношения W),
принимающий значения на отрезке [– 1, 1]. При этом:
а) wij = 0, если значение ei не зависит от
ej (влияние
отсутствует);
б)0 < wij £ 1 при положительном
влиянии ei на ej
(увеличение значения концепта-причины ei приводит к увеличению значения концепта-следствия ej
);
в) – 1 £ wij < 1 при отрицательном влиянии ei на ej
(увеличение значения ei приводит
к уменьшению значения ej).
Расчет системных показателей
Для
выполнения анализа построенной нечеткой когнитивной карты, помимо
непосредственно заданных причинно-следственных связей, необходимо учесть все
имеющиеся в системе опосредованные взаимовлияния факторов друг на друга. Это
позволяет сделать операция транзитивного замыкания, преобразующая исходную
матрицу интенсивности взаимовлияний W в транзитивно замкнутую матрицу Z,
элементами которой являются пары (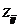 , ,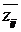 ), где ), где 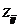 характеризует силу положительного
влияния, а характеризует силу положительного
влияния, а 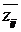 –
силу отрицательного влияния i-го концепта на j-й. На основе
матрицы Z могут быть рассчитаны следующие системные показатели
нечеткой когнитивной карты. –
силу отрицательного влияния i-го концепта на j-й. На основе
матрицы Z могут быть рассчитаны следующие системные показатели
нечеткой когнитивной карты.
Воздействие i-го концепта на j-й. Под воздействием понимается доминирующее по силе
влияние между концептами:
 . .
Влияние
(воздействие) i-го концепта на систему:
 . .
Влияние
(воздействие) системы на j-й концепт:
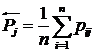 . .
Взаимное
(совместное) положительное влияние:
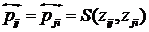 , ,
где S – операция S-нормы (как правило, используется максимум).
Консонанс
влияния i-го концепта на j-й. Показатель консонанса выражает меру доверия к знаку и
силе воздействия (чем выше консонанс, тем убедительнее мнение):
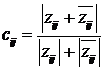 . .
Консонанс
влияния i-го концепта на систему:
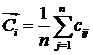 . .
Консонанс
влияния системы на j-й концепт:
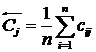 . .
Консонанс
взаимного влияния i-го и j-го концептов:
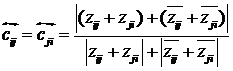 . .
Методика формирования множества альтернатив
Альтернатива представляет собой вектор воздействий
на управляемые концепты, так как только они доступны прямому влиянию
со стороны ЛПР. На остальные концепты, в том числе и на целевые, ЛПР может
влиять только опосредовано через управляемые. Значение управляемого концепта можно
увеличивать, уменьшать либо оставлять без изменений. Изменять значения каждого
концепта допускается в пределах заданной для него шкалы.
Разделим множество управляемых концептов на два
непересекающихся подмножества: подмножество способствующих концептов,
значения которых необходимо увеличивать, и подмножество препятствующих
концептов, значения которых необходимо уменьшать. Для определения того, какому
подмножеству принадлежит тот или иной концепт, воспользуемся системными
показателями когнитивной карты.
Обозначим:
EC – множество управляемых концептов;
ET – множество целевых концептов;
с – пороговое
значение консонанса (рекомендуется использовать с ≥ 0,5);
pd – пороговое значение прямого влияния концептов
(рекомендуется использовать pd ≥ 0,5);
pm – пороговое значение опосредованного влияния
концептов (рекомендуется использовать pm ≥ 0,2).
Пусть ei –
управляемый концепт (ei ∈ EC). Его принадлежность тому или иному подмножеству
устанавливается на основе следующих правил.
Правило
1
Если для всех целевых концептов (" ej ∈ ET) выполняется любое из условий:
a.
(pij ≥ pd) Ù (cij ≥ c), т.е. ei оказывает положительное влияние на ej с силой, не меньшей
pd, и консонанс
этого влияния не ниже с;
b.
(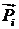 ≥ pm) Ù ( ≥ pm) Ù (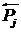 ≥ pm) Ù ( ≥ pm) Ù (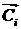 ≥ c) Ù ( ≥ c) Ù (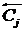 ≥ c),
т.е. ei оказывает положительное влияние на систему, а
система – положительное влияние на ej с силой, не меньшей pm, и консонанс этих влияний не ниже с; ≥ c),
т.е. ei оказывает положительное влияние на систему, а
система – положительное влияние на ej с силой, не меньшей pm, и консонанс этих влияний не ниже с;
c.
(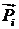 ≤ – pm) Ù ( ≤ – pm) Ù (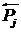 ≤ – pm) Ù ( ≤ – pm) Ù (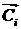 ≥ c) Ù ( ≥ c) Ù (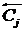 ≥ c), т.е. ei
оказывает отрицательное влияние на систему, а система – отрицательное
влияние на ei с силой, не меньшей pm,
и консонанс этих влияний не ниже с; ≥ c), т.е. ei
оказывает отрицательное влияние на систему, а система – отрицательное
влияние на ei с силой, не меньшей pm,
и консонанс этих влияний не ниже с;
d.
(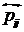 ≥ pd) Ù ( ≥ pd) Ù (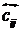 ≥ c), т.е. совместное положительное влияние
концептов ei и ej не
меньше p, и консонанс влияния не ниже с, ≥ c), т.е. совместное положительное влияние
концептов ei и ej не
меньше p, и консонанс влияния не ниже с,
и целевой концепт ej необходимо увеличить (уменьшить),
то концепт ei
является способствующим (препятствующим).
Правило
2
Если для всех целевых концептов (" ej ∈ ET) выполняется любое из условий:
a.
(pij ≤ – pd) Ù (cij ≥ c), т.е. ei оказывает отрицательное влияние на ej с силой, не меньшей pd, и консонанс
этого влияния не ниже с;
b.
(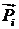 ≤ – pm) Ù ( ≤ – pm) Ù (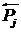 ≥ pm) Ù ( ≥ pm) Ù (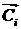 ≥ c) Ù ( ≥ c) Ù (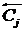 ≥ c),
т.е. ei оказывает отрицательное влияние на систему, а
система – положительное влияние на ej с силой, не меньшей pm, и консонанс этих влияний не ниже с; ≥ c),
т.е. ei оказывает отрицательное влияние на систему, а
система – положительное влияние на ej с силой, не меньшей pm, и консонанс этих влияний не ниже с;
c.
(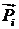 ≥ pm) Ù ( ≥ pm) Ù (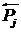 ≤ –pm) Ù ( ≤ –pm) Ù (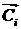 ≥ c) Ù ( ≥ c) Ù (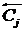 ≥ c), т.е. ei
оказывает положительное влияние на систему, а система – отрицательное
влияние на ei с силой, не меньшей pm,
и консонанс этих влияния не ниже с; ≥ c), т.е. ei
оказывает положительное влияние на систему, а система – отрицательное
влияние на ei с силой, не меньшей pm,
и консонанс этих влияния не ниже с;
d.
( ≥ pd) Ù ( ≥ pd) Ù (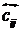 ≥ c), т.е. совместное отрицательное влияние
концептов ei и ej не
меньше p, и консонанс влияния не ниже с, ≥ c), т.е. совместное отрицательное влияние
концептов ei и ej не
меньше p, и консонанс влияния не ниже с,
и целевой
концепт ej необходимо увеличить (уменьшить),
то концепт ei
является препятствующим (способствующим).
Если концепт принадлежит только подмножеству
способствующих, то во всех генерируемых альтернативах его значение
необходимо увеличивать. Если концепт принадлежит только подмножеству
препятствующих, то во всех генерируемых альтернативах его значение необходимо
уменьшать. Если же концепт принадлежит обоим подмножествам, то необходимо
генерировать альтернативы, где его значение как уменьшается, так и
увеличивается.
Далее, на основе полного перебора всех возможных
комбинаций управляющих воздействий на концепты множества EC, генерируется базовое множество альтернатив Y,
из которого и будет осуществляться окончательный отбор.
Примечание: Вышеописанный алгоритм реализован только в
полнофункциональной версии. В демонстрационной версии путем полного перебора генерируется
не более 300 альтернатив.
Динамическое моделирование и отбор альтернатив
Для
получения прогноза развития ситуации при реализации различных альтернатив
используется математический аппарат импульсных процессов, который позволяет
прогнозировать значения концептов в дискретные моменты времени. Для
нечетких когнитивных карт предлагается следующая модификация модели импульсного
процесса:
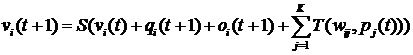 , ,
где: vi(
t) – значение концепта ei в момент времени t;
vi(
t + 1) – значение концепта ei в момент времени (t +
1);
qi(
t + 1) – внешнее воздействие на ei в момент времени (t + 1);
oi(t + 1) – управляющее воздействие на ei в момент (t + 1);
wij = w(ei
, ej) – интенсивность влияния между концептами
ei и ej;
pj(
t) – изменение значения ej в момент времени t;
Т – операция
Т-нормы (используется произведение);
S – операция
S-нормы (используется S-норма Лукасевича).
В
описанной модели импульсного процесса параметр t отражает протекание импульсного
процесса в нечеткой когнитивной карте (такты моделирования) и весьма слабо
соотносится с реальным временем в моделируемой системе. Кроме того, в
данной модели пренебрегается временными задержками при передаче воздействия
между концептами, и считается, что каждое воздействие происходит за единичное
время. Для получения нового устойчивого состояния моделируемой системы
целесообразно выполнять динамическое моделирование до значения t = 1,5N,
где N – количество концептов в когнитивной карте. Так как N – это
максимальная длина пути в нечеткой когнитивной карте, то при t = 1,5N
управляющие и внешние воздействия распространятся по всей карте.
Для оценки времени, которое понадобится управляемой системе для перехода в
новое состояние, необходима дополнительная информация о времени реакции системы
на различные управляющие воздействия.
Динамическое
моделирование выполняется для каждой альтернативы yi Î Y, и его результатом является набор конечных значений
концептов VR.
Отбор
сгенерированных этапе альтернатив выполняется в соответствии
с целью, заданной ЛПР. Как отмечалось ранее, целевое состояние системы
задается набором значений VT, которые должны получить целевые концепты в процессе
динамического моделирования (или максимально к ним приблизиться).
Отбор
альтернатив осуществляется путем выделения из базового множества альтернатив Y
подмножества недоминируемых альтернатив YN Ì Y.
Отношение доминирования основано на расстоянии | vTi – vRi |
от конечных значений концептов VR,
полученных в результате динамического моделирования по формуле , до
целевых значений концептов VT, а также силе управляющих воздействий на концепты при
реализации альтернатив.
Альтернатива
yi доминирует альтернативу yj,
если для всех целевых концептов ek Ì ET
выполняются неравенства:
| vTk – vRki | ≤ | vTk – vRkj |,
где
vTk – желаемое значение концепта ek,
vRki, vRkj – значения концепта ek, полученные в результате реализации альтернатив
соответственно yi и yj;
| yki | ≤ | ykj |, где
yki, ykj – управляющие воздействия на концепт ek при реализации альтернативы соответственно yi и yj.
Выделенное
множество недоминируемых альтернатив YN Ì Y, а также фактическое
множество конечных значений целевых концептов VR
передаются ЛПР для дальнейшего анализа и выбора наиболее предпочтительной
альтернативы.
|



